The Bohr equation is a fundamental concept in respiratory physiology, essential for anesthesiologists to assess ventilation efficiency. This equation provides a ratio of physiological dead space volume to tidal volume, offering critical insights into respiratory function during anesthesia and critical care. Understanding this equation helps optimize patient management, especially in cases where mechanical ventilation is involved.
The Bohr Equation: Definition and Formula
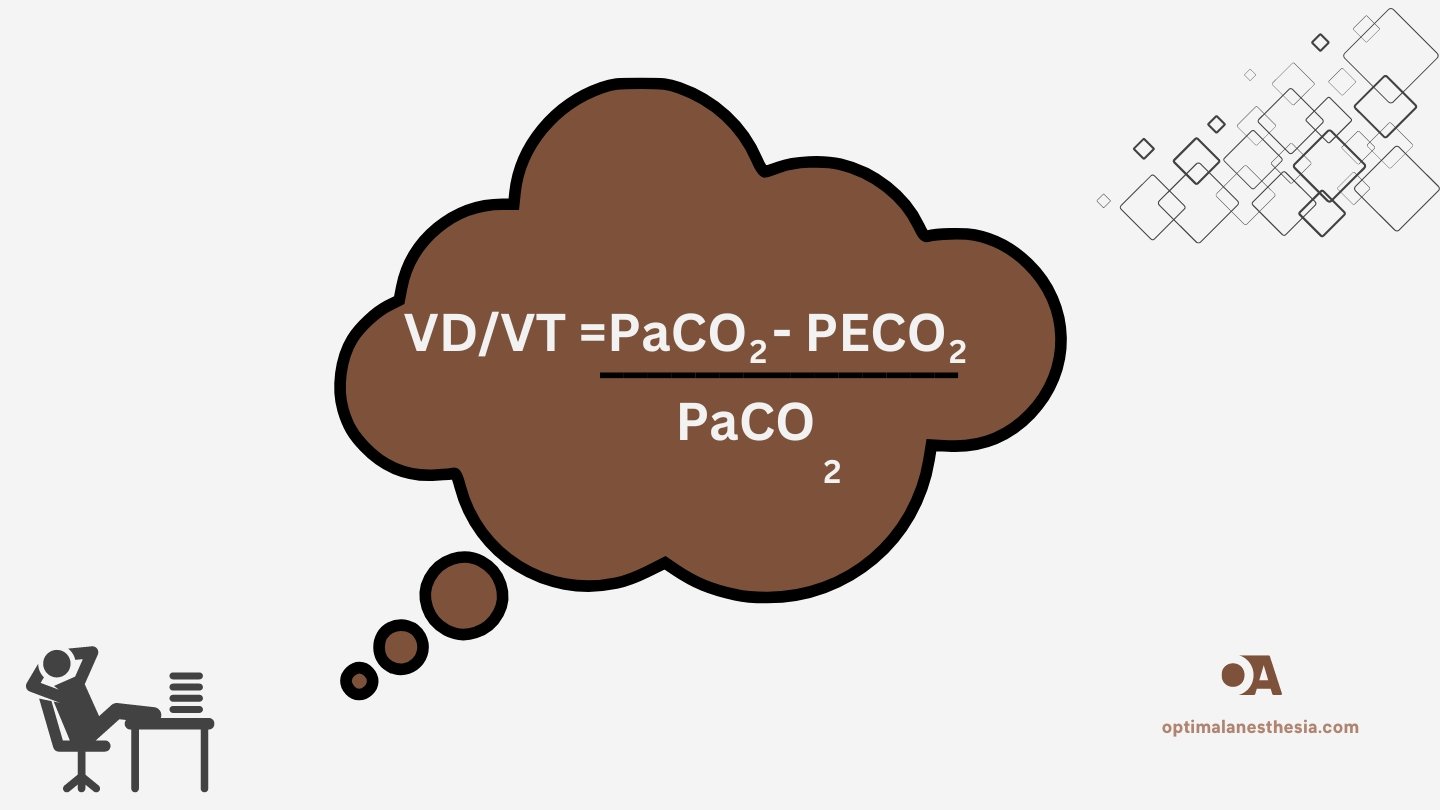
The Bohr equation is expressed as:

Where:
- VD is the physiological dead space volume.
- VT is the tidal volume.
- PaCO₂ is the arterial partial pressure of CO₂.
- PECO₂ is the partial pressure of CO₂ in mixed expired air.
The Bohr equation essentially quantifies the fraction of each breath that does not participate in gas exchange (dead space). It differentiates between alveolar gas and dead space gas based on CO₂ content, helping anesthesiologists identify inefficiencies in ventilation.
Clinical Relevance and Normal Values
In healthy individuals, the dead space volume accounts for approximately 30% of the tidal volume, resulting in a normal VD/VT ratio of about 0.3. This ratio tends to increase in patients with respiratory conditions, indicating less efficient ventilation. An increased VD/VT ratio suggests that a higher portion of the breath is “wasted,” meaning that it is not involved in gas exchange. This can result from various conditions, including pulmonary embolism, COPD, and acute respiratory distress syndrome (ARDS).
For anesthesiologists, monitoring the VD/VT ratio during anesthesia is crucial. An elevated ratio may signal a need for changes in ventilation settings or indicate underlying issues such as ventilation-perfusion (V/Q) mismatch, mechanical ventilation problems, or obstructed airways.
Physiological Basis of the Bohr Equation
The physiological concept behind the Bohr equation is that tidal volume (VT) comprises two parts:
- Dead space volume (VD): The portion of air that fills the airways and alveoli but does not participate in gas exchange.
- Alveolar volume (VT – VD): The portion of air that reaches the alveoli and is involved in gas exchange.
In essence, the dead space volume represents the air that remains in the respiratory passages (conducting airways) or alveoli that are ventilated but not perfused. Therefore, this air does not contribute to the exchange of gases (oxygen and carbon dioxide) with the blood. By calculating the VD/VT ratio, anesthesiologists can assess how efficiently the lungs are being ventilated and whether a portion of the breath is being “wasted” as dead space.
Clinical Applications of the Bohr Equation
- Assessing Ventilation Efficiency: The Bohr equation is crucial for evaluating how efficiently the lungs are ventilating. A rising VD/VT ratio suggests that ventilation is becoming less efficient, and adjustments to mechanical ventilation may be needed.
- Monitoring Respiratory Function During Anesthesia: During general anesthesia, changes in the VD/VT ratio may indicate problems with respiratory function. This is particularly useful in assessing patients under mechanical ventilation or those with compromised lung function.
- Detecting Ventilation-Perfusion Mismatches: An increased VD/VT ratio is often indicative of a ventilation-perfusion mismatch, where parts of the lungs are ventilated but not adequately perfused. This is common in conditions like pulmonary embolism or ARDS.
- Guiding Ventilation Strategies: The Bohr equation helps anesthesiologists optimize ventilation settings, especially in patients with severe lung diseases or during critical care management, such as in ARDS. Understanding the VD/VT ratio can help tailor ventilatory support to reduce dead space and improve gas exchange.
Practical Considerations
- Substitution of PaCO₂ for PACO₂: The original Bohr equation used alveolar CO₂ (PACO₂), but in clinical practice, arterial CO₂ (PaCO₂) is often substituted because it is easier to measure through arterial blood gas analysis.
- Assumptions of Zero Inspired CO₂: The Bohr equation assumes that the concentration of CO₂ in inspired air is negligible. However, in scenarios where this is not true (such as rebreathing or using certain ventilation systems), adjustments may be necessary.
- Limitations: While the Bohr equation is effective in assessing dead space, it does not differentiate between anatomical dead space (the conducting airways) and alveolar dead space (non-perfused alveoli). Further diagnostic tools may be needed to determine the exact cause of increased dead space.
Conclusion
For anesthesiologists, understanding the Bohr equation and its application is essential for effective patient management. It provides critical insights into ventilation efficiency, helping to identify ventilation-perfusion mismatches, optimize mechanical ventilation settings, and monitor respiratory function. Regular application of this equation, especially in complex cases such as ARDS or during major surgeries, can significantly improve patient outcomes.
References
- Nunn, J.F. (1993). Applied Respiratory Physiology. 4th ed. Oxford: Butterworth-Heinemann.
- West, J.B. (2012). Respiratory Physiology: The Essentials. 9th ed. Philadelphia: Lippincott Williams & Wilkins.
- Beachey, W. (2017). Respiratory Care Anatomy and Physiology. 5th ed. St. Louis: Elsevier.
- Enghoff, H. (1938). “Volumen inefficax. Bemerkungen zur Frage des Schadlichen Raumes.” Uppsala Laekareforen Forh. 44: 191-218.
- Robertson, H.T. (2015). “Dead Space: The Physiology of Wasted Ventilation.” European Respiratory Journal, 45(6), pp.1701-1703.
- Martin, A.D., & Smith, M.M. (2013). “Mechanical Ventilation and Respiratory Monitoring.” Current Opinion in Critical Care, 19(1), pp.20-24.
- Sahetya, S.K., & Brower, R.G. (2017). “Targeting Tidal Volumes in Acute Respiratory Distress Syndrome.” Respiratory Care, 62(6), pp.850-861.